Aristarchus of Samos
Quick Info
Samos, Greece
Greece
Biography
Aristarchus of Samos does not seem to have had the attention from historians of mathematics which he deserved until recent times. For example Heath begins Volume II of his history of Greek mathematics with the words [5]:-Historians of mathematics have, as a rule, given too little attention to Aristarchus of Samos. The reason is no doubt that he was an astronomer, and therefore it might be supposed that his work would have no sufficient interest for the mathematician. The Greeks knew better; they called him 'Aristarchus the mathematician'.However the fact that he was known as an astronomer rather than a mathematician is rather countered by Neugebauer's claim that his work [6]:-
... is a purely mathematical exercise which has ... little to do with practical astronomy ...Zhitomirskii, in [14], states:-
Aristarchus of Samos is a little-known but often cited precursor of Copernicus. All information about him derives from a handful of scattered references in Classical writers, plus a short treatise of his which does not mention heliocentrism. Accordingly historians often mention him, cite one or two facts and move on to another subject - after providing a few words of explanation that reveal much about the historians' biases.The paper [14] then makes a serious attempt to remedy what the author considers to be the shortcomings of other historians. Let us try in this article to do more than 'mention one or two facts' and to indicate both the magnitude and originality of Aristarchus's achievements and also his role in the development of mathematical astronomy.
Aristarchus was certainly both a mathematician and astronomer and he is most celebrated as the first to propose a sun-centred universe. He is also famed for his pioneering attempt to determine the sizes and distances of the sun and moon. We shall look at these two achievements below.
Aristarchus was a student of Strato of Lampsacus, who was head of Aristotle's Lyceum. However, it is not thought that Aristarchus studied with Strato in Athens but rather that he studied with him in Alexandria. Strato became head of the Lyceum at Alexandria in 287 BC and it is thought that Aristarchus studied with him there starting his studies shortly after that date.
Aristarchus is mentioned by Vitruvius (1st century BC) who was famous as a Roman architect and engineer. Vitruvius was the author of the important treatise De architectura (On Architecture) and in this work he lists men who have been knowledgeable across all branches of science (see for example [3], [4], or [5]):-
Men of this type are rare, men such as were, in past times, Aristarchus of Samos, Philolaus and Archytas of Tarentum, Apollonius of Perga, Eratosthenes of Cyrene, Archimedes and Scopinas of Syracuse, who left to posterity many mechanical and gnomonic appliances which they invented and explained on mathematical principles.Of course there is the immediate question of what Aristarchus invented, and Vitruvius explains that he invented a sundial in the shape of a hemispherical bowl with a pointer to cast shadows placed in the middle of the bowl.
There is little existing evidence concerning the origin of Aristarchus's belief in a heliocentric system. We know of no earlier hypothesis of this type but in fact the theory was not accepted by the Greeks so apparently never had any popularity. We only know of Aristarchus's theory because of a summary statement made in Archimedes' The Sand-Reckoner and a similar reference by Plutarch. Archimedes wrote (see for example [3], [4], or [5], or see [1] for a shorter quote):-
You King Gelon are aware the 'universe' is the name given by most astronomers to the sphere the centre of which is the centre of the earth, while its radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account as you have heard from astronomers. But Aristarchus has brought out a book consisting of certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than the 'universe' just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun on the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface.Archimedes having reported the views of Aristarchus, criticised those views as giving mathematically meaningless proportions. In fact the way that Aristarchus expresses his proportions is, according to Heath, similar to other expressions which occur in Greek writings and indicated that Aristarchus considered that the radius of the sphere of the fixed stars was infinitely large compared with the orbit of the earth. Of course, Aristarchus had to make some such assumption, for otherwise parallax effects would be visible.
Plutarch gives us a little extra information, for he reports that Aristarchus followed Heraclides of Pontus in believing that the apparent daily rotation of the fixed stars was due to the rotation of the earth on its axis.
The only surviving work of Aristarchus, On the Sizes and Distances of the Sun and Moon, is not based on the sun centred theory and unfortunately his work on that sun centred theory referred to by Archimedes has been lost. On the Sizes and Distances of the Sun and Moon provides the details of his remarkable geometric argument, based on observation, whereby he determined that the Sun was about 20 times as distant from the Earth as the Moon, and 20 times the Moon's size. Both these estimates were an order of magnitude too small, but the fault was in Aristarchus's lack of accurate instruments rather than in his correct method of reasoning.
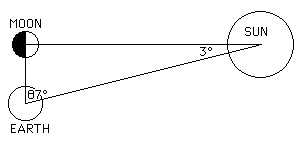
The diagram shows an argument used by Aristarchus. He knew that the moon shines by reflected sunlight, so he argued, if one measured the angle between the moon and sun when the moon is exactly half illuminated then one could compute the ratio of their distances. Aristarchus estimated that the angle at the time of half illumination was 87° so the ratio of the distances is sin 3°. Of course, we have translated this into modern notation for Aristarchus did not use degrees nor had trigonometry been invented so he did not have the sine function at his disposal. However this is in effect the calculation he made, correct in principle yet almost impossibly difficult to observe in practice since determining the moment at which half illumination of the moon occurs can only be very inaccurately found.
Aristarchus was then faced with calculating an approximation for what is in our notation sin 3°. He obtained the inequality
and deduced that the sun was between 18 to 20 times as far away as the moon. In fact at the moment of half illumination the angle between the moon and the sun is actually 89° 50' and the sun is actually about 400 times further away than the moon.
Rather strangely Aristarchus uses values for the angle subtended by the sun and moon to be 2°. This figure is quite inaccurate as it is four times too large. He correctly uses the evidence of eclipses to state that the sun and moon subtend the same angle. However, Archimedes quotes a value of for the angle subtended by the sun and attributes this figure to Aristarchus. We can only assume that Aristarchus wrote On the Sizes and Distances of the Sun and Moon early in his career, then later on he adopted his hypothesis of a sun centred universe and computed a much more accurate value of the angle subtended by the sun. One has to assume Aristarchus was able to develop instruments to make accurate astronomical measurements later in his career.
Neugebauer argues in [6] that Aristarchus was not interested in accurate astronomical data (since he could have easily done very much better had he been interested). Rather Neugebauer suggests, Aristarchus was only interested in the mathematical theory behind finding the distances and diameters. He was showing that such measurements could be made and, since he succeeds in showing this, his work is of major importance. As Neugebauer writes in [6]:-
... the power of the mathematical approach to astronomical problems has been drastically demonstrated, in the same sense as Eudoxus, a century earlier, constructed cinematic models which could be related to planetary motions without solving a single specific problem.There are one or two other references to work of Aristarchus which have been investigated recently. For example in [7] the authors interpret:-
... a difficult passage in an anonymous commentary written in Greek during the 2nd century AD on Book 20 of Homer's Odyssey. ... the [anonymous] author quotes Aristarchus of Samos citing Thales and Heraclitus in order to support his thesis [of] solar eclipses ... [His] thesis concerning the times when solar eclipses may occur rests on an analysis of Greek and Egyptian calendrical conventions, rather than on an appeal to observation of solar eclipses.
References (show)
- W H Stahl, Biography in Dictionary of Scientific Biography (New York 1970-1990).
See THIS LINK. - Biography in Encyclopaedia Britannica.
http://www.britannica.com/biography/Aristarchus-Of-Samos - T L Heath, Aristarchus of Samos (Oxford, 1913).
- T L Heath, Aristarchus of Samos. The ancient Copernicus : Reprint of the 1913 original (New York, 1981).
- T L Heath, A history of Greek mathematics I, II (Oxford, 1931).
- O Neugebauer, A History of Ancient Mathematical Astronomy (3 Vols.) (Berlin-Heidelberg-New York, 1975).
- A C Bowen and B R Goldstein, Aristarchus, Thales, and Heraclitus on solar eclipses : an astronomical commentary on P Oxy 53.3710 cols. 2.33-3.19, Physis Riv. Internaz. Storia Sci. (N.S.) 31 (3) (1994), 689-729.
- M Gabriel, Les theories heliocentriques dans l'antiquite grecque, Ciel et terre : bulletin de la Societe belge d'astronomie et revue populaire d'astronomie, de meteorologie et de physique du globe 104 (1988), 107-108.
- O Gingerich, Did Copernicus owe a debt to Aristarchus?, J. Hist. Astronom. 16 (1) (1985), 37-42.
- M Milankovitch, Aristarchos und Apollonios. Das heliozentrische und das geozentrische Weltsystem des klassischen Altertums, Acad. Serbe Sci. Publ. Inst. Math. 9 (1956), 79-92.
- O Neugebauer, Archimedes and Aristarchus, Isis 34 (1942), 4-6.
- R von Erhardt and E von Erhardt-Siebold, Archimedes' Sand-Reckoner. Aristarchos and Copernicus, Isis 33 (1942), 578-602.
- B E Wall, Anatomy of a precursor : the historiography of Aristarchos of Samos, Studies in Hist. and Philos. Sci. 6 (3) (1975), 201-228.
- S V Zhitomirskii, The heliocentric hypothesis of Aristarchos of Samos and ancient cosmology (Russian), Istor.-Astronom. Issled. No. 18 (1986), 151-160.
Additional Resources (show)
Other pages about Aristarchus:
Other websites about Aristarchus:
Honours (show)
Honours awarded to Aristarchus
Cross-references (show)
- History Topics: Greek astronomy
- History Topics: Greek number systems
- History Topics: The Size of the Universe
- History Topics: Timekeeping in the Ancient World: Sundials
- Other: 2009 Most popular biographies
- Other: Jeff Miller's postage stamps
- Other: Most popular biographies – 2024
- Other: Popular biographies 2018
- Other: The Reaches of the Milky Way
- Other: The Structure of the Solar System
Written by J J O'Connor and E F Robertson
Last Update April 1999
Last Update April 1999
